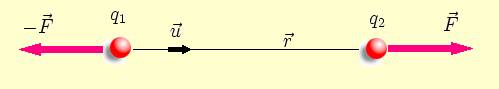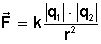Fuerza Eléctrica - Ley de Coulomb

LEY DE COULUMB

La Ley de Coulomb, que establece cómo es la fuerza entre dos cargas eléctricas puntuales, constituye el punto de partida de la Electrostática como ciencia cuantitativa.

Fue descubierta por Priestley en 1766, y redescubierta por Cavendish pocos años después, pero fue Coulomb en 1785 quien la sometió a ensayos experimentales directos.

Entendemos por carga puntual una carga eléctrica localizada en un punto geométrico del espacio. Evidentemente, una carga puntual no existe, es una idealización, pero constituye una buena aproximación cuando estamos estudiando la interacción entre cuerpos cargados eléctricamente cuyas dimensiones son muy pequeñas en comparación con la distancia que existen entre ellos.

La Ley de Coulomb dice que "la fuerza electrostática entre dos cargas puntuales es proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia que las separa, y tiene la dirección de la línea que las une. La fuerza es de repulsión si las cargas son de igual signo, y de atracción si son de signo contrario".

En términos matemáticos, esta ley se refiere a la magnitud F de la fuerza que cada una de las dos cargas puntuales q 1 y q 2 ejerce sobre la otra separadas por una distancia r y se expresa en forma de ecuación como:

Elian Hernando Gil Sierra 

Hernan Dario Gomez

Arley Eduardo Buenaver

La balanza de torsión

En uno de sus trabajos más famosos, Coulomb utilizó hebras de diversos materiales para perfeccionar la balanza de torsión. Este instrumento consiste en una barra que cuelga de una fibra que es capaz de retorcerse. Si la barra gira, la fibra tiende a llevarla a su posición original. Si se conoce la fuerza de torsión que la fibra ejerce sobre la barra, se logra un método muy sensible para medir fuerzas.

Tipos

Los materiales más empleados como torsores suelen tener una forma alargada en forma de chapa, cable, barra, etc.

• Gomas de torsión: se emplean en los relojes de péndulo de torsión.

• Barras de torsión : se emplean para dar soporte a los componentes de suspensión (Automóvil) de los automóviles, permitiendo que estos componentes (que indirectamente se soportan sobre las ruedas) sean las responsables de amortiguar los movimientos verticales cuando se conduce un vehículo.

Usos y aplicaciones

La balanza de torsión es un dispositivo creado por el físico Charles-Augustin de Coulomb en el año 1777, con el objeto de medir fuerzas débiles. Coulomb empleó la balanza para medir la fuerza electrostática entre dos cargas. El encontró que la fuerza electrostática entre dos cargas puntuales es directamente proporcional al producto de las magnitudes de las cargas eléctricas e inversamente al cuadrado de la distancia entre las cargas. A este descubrimiento lo denominó Ley de coulomb.

La balanza de torsión consiste en dos bolas de metal sujetas por los dos extremos de una barra suspendida por un cable, filamento o chapa delgada. Para medir la fuerza electrostática se puede poner una tercera bola cargada a una cierta distancia. Las dos bolas cargadas se repelen/atraen unas a otras, causando una torsión de un cierto ángulo. De esta forma se puede saber cuánta fuerza, en newton (unidad), es requerida para torsional la fibra un cierto ángulo.

Una balanza de torsión se empleó en el experimento de Cavendish realizado en 1789 para medir la constante de gravedad con la mayor precisión posible. Las balanzas de torsión se siguen empleando hoy en día en los experimentos de física.

Referencias.

·         Jfinternational

·         Wikipedia

Angélica Silva Pinto

Yohan Suarez Barajas

Brayan Suarez Duarte

FOTOCOPIADORA

Una aplicación tecnológica de las fuerzas eléctricas de atracción es la fotocopiadora. En ella las regiones del tambor de imágenes se cargan positivamente y atraen a partículas con carga negativa del toner. Estas partículas conforman un polvillo negro, que dibuja la imagen cuando se adhiere a la hoja de la copia.

Etapas en el funcionamiento de una fotocopiadora:

1: El documento original es barrido por un rayo de luz, que refleja o proyecta la imagen sobre un tambor foto-sensible. Las áreas oscuras quedan con carga positiva después de la exposición.

2: Las partículas del toner, con carga negativa, son atraídas por el área de carga positiva

3: Se carga una hoja de papel blanco, preparada para recibir la copia 4: Las partículas se adhieren sobre el papel cuando éste rueda sobre el toner, produciendo la copia.

Nicolas Johan Sebastian Silva Diaz.
Daniel de Jesús Martinez Vega.
Fernando Andrés Pérez Pallares.

Referencias.
http://intercentres.edu.gva.es/iesleonardodavinci/Fisica/Campo-electrico/Electrico10.htm

La intensidad de las fuerzas eléctricas es mayor que la de la fuerza gravitatoria a nivel atómico

La fuerza eléctrica con que se repelen dos protones en un átomo es aproximadamente, un billón de billones de billones (1036) más intensa que la gravitacional con que se atraen. Para comprender este hecho supongamos que en una escala de intensidades la fuerza gravitatoria tiene magnitud 1, entonces la fuerza eléctrica tendrá un valor de 1036: un uno seguido de 36 ceros.

Sabías que…

- Los cuerpos, como la Tierra,  la mesa, el lápiz o nosotros mismos, tienen exactamente la misma cantidad de carga positiva que de carga negativa. Es decir: las cargas están equilibradas,  los cuerpos son eléctricamente neutros, por ello no hay fuerzas eléctricas entre ellos y se dejan sentir las gravitatorias, aunque sean mucho más débiles.

Imagen 1.  Comparación entre fuerza eléctrica y fuerza gravitatoria.

Tomado de: http://e-ducativa.catedu.es

Elian Hernando Gil Sierra 

Hernan Dario Gomez

Arley Eduardo Buenaver

Fuerzas eléctricas en la biología molecular

Sabemos que nuestro organismo esta formado por millones de células. Éstas todo el tiempo interactúan entre si y tienen una energía cinética debido a su movimiento. Es aquí donde entran al juego las fuerzas electrostáticas que son las causantes de estos movimientos aparentemente aleatorios de las células.

Pero gracias a las fuerzas electrostáticas todo lo que sucede al interior de las células que aparentemente es perfecto y mágico es gracias a la fuerzaelectrostática entre distintas moléculas. Esel ejemplo del ADN.

El ADN contiene la información que nos caracteriza y la podemos encontrar en los cromosomas. El ADN adquiere la forma de una doble hélice enrollada, pero si se mira mas adentro el ADN esta hecho de pequeñas moléculas llamadas nucleótidos (Adenina, Guanina, Tianina, Citosina). En ésta imagen podemos ver el ADN y sus nucleótidos:

A lo que se quiere llegar es que estas dos hebras están unidas por fuerzas electrostáticas es decir la atracción entre cargas negativas y positivas en este caso los nucleotidos. Por eso vemos la organización o unión de tipo A (Adenina) con T (Tianina) y de G (Guanina) con C (Citosina). Cabe recordar que estas uniones son efectivas cuando las cargas (Los nucleótidos) se encuentran muy cercanos ente si, ya que la fuerza de atracción disminuye con la distancia (F ⇀ 1/r^2).

En el proceso de duplicación del ADN los nucleótidos y las hélices se separan gracias a la interacción e otras encimas que permiten separar están moléculas. A la hora de reorganizarse o duplicarse las fuerzas eléctricas juegan un papel muy importante ya que ponen orden a la formación de nuevas cadenas genéticas. A veces éstas fuerzas no son lo suficientemente fuertes y se producen errores que es lo que conocemos como enfermedades cromosómicas.


Fuentes:
Douglas C. Giancoli. Física para ciencias e ingeniería Volumen II. Pearson educación, México, 2009.

Jhorman González Pilonieta
Cristian Serrano Ramos

Fuerza eléctrica aplicada al Tren de levitación magnética

Transrapid (Shangai, China)

La levitación magnética es un sistema usado principalmente en trenes, este consiste en usar muchos imanes para que por medio de las fuerzas eléctricas este se mantenga en el aire, estos vehículos de propulsión magnética flotan en la vía y alcanzan velocidades de hasta 500 km/h y no tiene conductor.

Shanghai Transrapid 29 December 2004

El tren (maglev) se enrolla alrededor de una guía en forma de T bordeada con "rieles guía" de metal delgados.Las computadoras y los sensores controlan los imanes de soporte y guía del tren estos mantienen el tren a tres octavos de pulgada de su riel de guía en cada lado y aproximadamente a seis pulgadas por encima de la guía. La parte inferior de la guía también contiene bobinados que cuando se electrifican con corriente alterna generan su propio conjunto de campos magnéticos que atraen continuamente los imanes de soporte. Los bobinados de la pista se conectan y desconectan por sección, a medida que pasa el tren, evitando la necesidad de energizar continuamente toda la ruta.

Esquema con las fuentes de fuerzas magnéticas de suspensión.

En china los ingenieros trabajan otro tipo de modelo maglev intentando usar la repulsión en vez de la atracción, en este sistema la levitación no toma el control hasta que el tren alcanza las 25 millas por hora (40 kilómetros por hora). Por lo tanto, usa ruedas retráctiles al principio y al final de una carrera.

El diseño permite una brecha más amplia entre el tren y la vía, agrega Rote, proporcionando una pista más indulgente, si se deforma debido a la actividad sísmica.

Fuentes:

"Un tren japonés maglev bate récord de velocidad, con 603 km/h". EuropaPress. 21 de abril de        2015. Consultado el 21 de abril de 2015
"Los trenes magnéticos recogen impulso". National Geography news 

"Trenes del futuro". Super estructuras. National geography

Chrystiam Camilo Esquivel Rangel

Bryan Fernando Carvajal Torres

Karen Lucia Castellanos Caicedo

La fuerza eléctrica

F, start subscript, 2, end subscript, with, vector, on top, equals, 4, point, 5, times, 10, start superscript, 10, end superscript, space, angle, space, 6, point, 9, degree, space, n, e, w, t, o, n, s

Ejemplo: fuerza entre una recta cargada y una carga

Una recta cargada de $L$L metros de longitud tiene una carga total de $Q$Q. Supón que la carga total, $Q$Q, está uniformemente distribuida a lo largo de la recta. Una carga puntual $q$q se encuentra a una distancia de $a$a metros de uno de los extremos la recta, en la misma dirección que esta.

Encuentra la fuerza total sobre la carga $q$q colocada en la misma dirección en la que apunta la recta cargada.

La recta contiene una carga total de $Q$Q coulombs. Podemos abordar este problema al pensar la recta como un montón de cargas individuales colocadas una junto a la otra. Para calcular la fuerza total sobre la carga $q$q debida a la recta, sumamos (integramos) las fuerzas individuales debidas a cada carga puntual en la recta.

Definimos la densidad de carga en la recta como $\dfrac{Q}{L}$start fraction, Q, divided by, L, end fraction coulombs/metro.

El concepto de "densidad de carga" nos permite expresar la cantidad de carga, $\text dQ$d, Q, en un pequeño segmento de la recta, $\text dx$d, x, como

$\text dQ = \dfrac{Q}{L}\,\text dx$d, Q, equals, start fraction, Q, divided by, L, end fraction, space, d, x

El término $\text dQ$d, Q es lo suficientemente pequeño para aproximar una carga puntual, lo que nos permite aplicar la ley de Coulomb. Podemos determinar la dirección de la fuerza inmediatamente: la fuerza sobre $q$q debida a cada $\text dQ$d, Q va en la misma dirección que la recta que une $q$q con $\text dQ$d, Q. Ya que determinamos la dirección, calculamos la magnitud de la fuerza:

$\text dF = \dfrac{1}{4\pi\epsilon_0}\dfrac{q \,\text dQ}{x^2}$

El numerador multiplica las dos cargas, $q$q y $\text dQ$d, Q; el denominador $x$x representa la distancia entre las dos cargas.

Para encontrar la fuerza total, sumamos todas la fuerzas debidas a cada $\text dQ$d, Q al integrar del extremo cercano ($\text a$a) al extremo lejano de la recta ($\text a + \text L$a, plus, L).

$\displaystyle F = \int_a^{a+L} \text d\vec F = \int_a^{a+L} \dfrac{1}{4\pi\epsilon_0}\dfrac{q \,\text dQ}{x^2}$

Esta ecuación incluye tanto $x$x como $\text dQ$d, Q como variables. Para reducirla a una sola variable independiente, reemplazamos el término $\text dQ$d, Q por la expresión $Q/L \,\text dx$Q, slash, L, space, d, x determinada arriba; así,

$\displaystyle F = \int_a^{a+L} \dfrac{1}{4\pi\epsilon_0} \dfrac{qQ}{L} \dfrac{1}{x^2} \text{d}x$

Sacamos de la integral todo lo que no depende de $x$x.

$\displaystyle F = \dfrac{1}{4\pi\epsilon_0} \dfrac{qQ}{L} \int_a^{a+L}\dfrac{1}{x^2} \text{d}x$

Y resolvemos la integral 

[Pista]

$x$x$\displaystyle \int x^n \text d x = \dfrac{x^{n+1}}{n+1}$integral, x, start superscript, n, end superscript, d, x, equals, start fraction, x, start superscript, n, plus, 1, end superscript, divided by, n, plus, 1, end fraction$n \neq -1$n, does not equal, minus, 1$n = -2$n, equals, minus, 2

$\displaystyle \int_a^{a+L} x^{-2} \text dx = \dfrac{x^{-2+1}}{-2+1} = \dfrac{x^{-1}}{-1} = -\dfrac{1}{x}$integral, start subscript, a, end subscript, start superscript, a, plus, L, end superscript, x, start superscript, minus, 2, end superscript, d, x, equals, start fraction, x, start superscript, minus, 2, plus, 1, end superscript, divided by, minus, 2, plus, 1, end fraction, equals, start fraction, x, start superscript, minus, 1, end superscript, divided by, minus, 1, end fraction, equals, minus, start fraction, 1, divided by, x, end fraction

$-\dfrac{1}{x}\bigg|_a^{a+L} = -\left [\ \dfrac{1}{(a+L)} - \dfrac{1}{a}\,\right ] = \dfrac{1}{a} - \dfrac{1}{(a+L)}$minus, start fraction, 1, divided by, x, end fraction, vertical bar, start subscript, a, end subscript, start superscript, a, plus, L, end superscript, equals, minus, open bracket, space, start fraction, 1, divided by, left parenthesis, a, plus, L, right parenthesis, end fraction, minus, start fraction, 1, divided by, a, end fraction, space, close bracket, equals, start fraction, 1, divided by, a, end fraction, minus, start fraction, 1, divided by, left parenthesis, a, plus, L, right parenthesis, end fraction

$\dfrac{1}{a} \left ( \dfrac{a+L}{a+L}\right ) - \dfrac{1}{(a+L)} \left ( \dfrac{a}{a} \right ) = \dfrac{(a+L)-a}{a(a+L)}$start fraction, 1, divided by, a, end fraction, left parenthesis, start fraction, a, plus, L, divided by, a, plus, L, end fraction, right parenthesis, minus, start fraction, 1, divided by, left parenthesis, a, plus, L, right parenthesis, end fraction, left parenthesis, start fraction, a, divided by, a, end fraction, right parenthesis, equals, start fraction, left parenthesis, a, plus, L, right parenthesis, minus, a, divided by, a, left parenthesis, a, plus, L, right parenthesis, end fraction

$a$a

$\displaystyle \int_a^{a+L} x^{-2} \text dx = \dfrac{L}{a(a+L)}$integral, start subscript, a, end subscript, start superscript, a, plus, L, end superscript, x, start superscript, minus, 2, end superscript, d, x, equals, start fraction, L, divided by, a, left parenthesis, a, plus, L, right parenthesis, end fraction

$\displaystyle \vec F = \dfrac{1}{4\pi\epsilon_0} \dfrac{qQ}{\cancel L} \dfrac{\cancel L}{a(a+L)}$

$\large F = \dfrac{1}{4\pi\epsilon_0} \dfrac{qQ}{a(a+L)}$

Algunas cosas a observar sobre la solución:

• El numerador es el producto de la carga de prueba y la carga total de la recta, lo cual tiene sentido.
• El denominador tiene la forma "$\text{distancia}^2$d, i, s, t, a, n, c, i, a, start superscript, 2, end superscript", generada por una combinación de la distancia en los extremos cercano y lejano de la recta. La forma $a(a+L)$a, left parenthesis, a, plus, L, right parenthesis del denominador resulta de la geometría particular de este ejemplo.
• Si la carga puntual $q$q se mueve muy lejos de la recta, $L$L se vuelve insignificante en comparación con $a$a, y el denominador se aproxima a $a^2$a, start superscript, 2, end superscript. Por lo tanto, a una distancia muy grande, la recta comienza a parecer una carga puntual lejana y, como uno esperaría, la ecuación se aproxima a la ley de Coulomb para dos cargas puntuales.

Vamos a hacer una par de ejercicios más de electrostática que involucran objetos cargados con geometrías sencillas. Después de estos, los cálculos se vuelven muy intrincados, por lo que una estrategia común con geometrías complicadas es: separar la geometría en versiones más sencillas que sepamos hacer y luego combinar las respuestas.

Estrategias para aplicar la ley de Coulomb

La ley de Coulomb es una buena elección para situaciones que involucran cargas puntuales y geometrías simétricas sencillas como rectas o esferas cargadas.

Ya que la ley de Coulomb se basa en fuerzas generadas por pares de cargas, cuando te enfrentes a múltiples (más de dos) cargas puntuales:

1. Trabaja por separado la fuerza entre cada par de cargas.
2. Concluye con una suma de vectores para combinar las fuerzas debidas a la interacción de cada par en una sola fuerza resultante.

Para una situación con carga distribuida, modela creativamente la carga distribuida como una colección de cargas puntuales:

1. Define un pequeño término $\text dQ$d, Q que represente una carga infinitesimal dentro de la región de carga distribuida.
2. Trabaja las fuerzas entre los pares formados por la carga puntual y cada $\text dQ$d, Q.
3. Suma las fuerzas con una integral. Esta es una suma vectorial que culmina en la fuerza resultante.

Bibliografia:
https://es.khanacademy.org/science/electrical-engineering/ee-electrostatics/ee-electric-force-and-electric-field/a/ee-electric-force

JAVIER ANDRES PEREZ GOMEZ

MARIA ALEJANDRA GUTIERREZ PALENCIA

WILMER CACERES